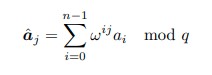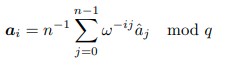Hardware Design for Post-Quantum Cryptography Polynomial Multiplier

NTT Algorithm Process

Multiply two polynomials \( A(x) \) and \( B(x) \):

NTT Formula

INTT Formula

Enter a modulus \( q \):

\( q \equiv 1 \pmod{4} \), where \( n = 4 \).

Choose a primitive root \( \omega \):

Selected \( q \):

Enter the first 4-term polynomial coefficients (comma-separated): Enter the second 4-term polynomial coefficients (comma-separated):

Formula:

\( \hat{A}_k = \sum_{j=0}^{n-1} a_j \cdot \omega^{j \cdot k} \mod q \)

Steps for \( [1, 2, 3, 4] \):

\( \hat{A}_0 = (1 + 2 + 3 + 4) \mod 17 = 10 \)
\( \hat{A}_1 = (1 \cdot 1 + 2 \cdot 13 + 3 \cdot 16 + 4 \cdot 4) \mod 17 = 6 \)
\( \hat{A}_2 = (1 \cdot 1 + 2 \cdot 16 + 3 \cdot 1 + 4 \cdot 16) \mod 17 = 15 \)
\( \hat{A}_3 = (1 \cdot 1 + 2 \cdot 4 + 3 \cdot 16 + 4 \cdot 13) \mod 17 = 7 \)

Result: \( \text{NTT}(A) = [10, 6, 15, 7] \)

Formula:

\( \hat{C}_k = \hat{A}_k \cdot \hat{B}_k \mod q \)

Steps:

Result: \( \hat{C} = [15, 2, 4, 15] \)

Formula:

\( a_j = n^{-1} \cdot \sum_{k=0}^{n-1} \hat{C}_k \cdot \omega^{-j \cdot k} \mod q \)

Steps:

\( a_0 = 13 \cdot (15 + 2 + 4 + 15) \mod 17 = 9 \)
\( a_1 = 13 \cdot (15 \cdot 1 + 2 \cdot 4 + 4 \cdot 16 + 15 \cdot 13) \mod 17 = 11 \)
\( a_2 = 13 \cdot (15 \cdot 1 + 2 \cdot 16 + 4 \cdot 1 + 15 \cdot 16) \mod 17 = 9 \)
\( a_3 = 13 \cdot (15 \cdot 1 + 2 \cdot 13 + 4 \cdot 16 + 15 \cdot 4) \mod 17 = 3 \)

Result: \( \text{INTT Result} = [9, 11, 9, 3] \)

In the ring \( \mathbb{Z}_{17}[x]/(x^4 - 1) \):

\( [1, 2, 3, 4] \cdot [1, 2, 3, 4] = [9, 11, 9, 3] \)